Parallelizing simr::powercurve() in R

2021 R, research methods

The powercurve function from the R package ‘simr’ (Green & MacLeod, 2016) can incur very long running times when the method used for the calculation of p values is Kenward-Roger or Satterthwaite (see Luke, 2017). Here I suggest three ways for cutting down this time.

  1. Where possible, use a high-performance (or high-end) computing cluster. This removes the need to use personal computers for these long jobs.

  2. In case you’re using the fixed() parameter of the powercurve function, and calculating the power for different effects, run these at the same time (‘in parallel’) on different machines, rather than one after another.

  3. Parallelize the breaks argument. The breaks argument of the powercurve function allows the calculation of power for different levels of the grouping factor passed to along. Some grouping factors are participant, trial and item. The breaks argument sets the different sample sizes for which power will be calculated. Parallelizing breaks is done by running each number of levels in a separate function. When each has been run and saved, they are combined to allow the plotting. This procedure is demonstrated below.

Parallelizing breaks

Let’s do a minimal example using a toy lmer model. A power curve will be created for the fixed effect of x along different sample sizes of the grouping factor g.

Notice that the six sections of the power curve below are serially arranged, one after another. In contrast, to enable parallel processing, each power curve would be placed in a single script, and they would all be run at the same time.

Although the power curves below run in a few minutes, the settings that are often used (e.g., a larger model; fixed('x', 'sa') instead of fixed('x'); nsim = 500 instead of nsim = 50) take far longer. That is where parallel processing becomes useful.1

library(lme4)
library(simr)

# Toy model with data from 'simr' package
fm = lmer(y ~ x + (x | g), data = simdata)

# Extend sample size of `g`
fm_extended_g = extend(fm, along = 'g', n = 12)

# Parallelize `breaks` by running each number of levels in a separate function.

# 4 levels of g
pwcurve_4g = powerCurve(fm_extended_g, fixed('x'), along = 'g', breaks = 4, 
                        nsim = 50, seed = 123, 
                        # No progress bar
                        progress = FALSE)

# 6 levels of g
pwcurve_6g = powerCurve(fm_extended_g, fixed('x'), along = 'g', breaks = 6, 
                        nsim = 50, seed = 123, 
                        # No progress bar
                        progress = FALSE)

# 8 levels of g
pwcurve_8g = powerCurve(fm_extended_g, fixed('x'), along = 'g', breaks = 8, 
                        nsim = 50, seed = 123, 
                        # No progress bar
                        progress = FALSE)

# 10 levels of g
pwcurve_10g = powerCurve(fm_extended_g, fixed('x'), along = 'g', breaks = 10, 
                        nsim = 50, seed = 123, 
                        # No progress bar
                        progress = FALSE)

# 12 levels of g
pwcurve_12g = powerCurve(fm_extended_g, fixed('x'), along = 'g', breaks = 12, 
                        nsim = 50, seed = 123, 
                        # No progress bar
                        progress = FALSE)


Having saved each section of the power curve, we must now combine them to be able to plot them together (if you wish to automatise this procedure, consider this function).

# Create a destination object using any of the power curves above.
all_pwcurve = pwcurve_4g

# Combine results
all_pwcurve$ps = c(pwcurve_4g$ps[1], pwcurve_6g$ps[1], pwcurve_8g$ps[1], 
                   pwcurve_10g$ps[1], pwcurve_12g$ps[1])

# Combine the different numbers of levels.
all_pwcurve$xval = c(pwcurve_4g$nlevels, pwcurve_6g$nlevels, pwcurve_8g$nlevels, 
                     pwcurve_10g$nlevels, pwcurve_12g$nlevels)

print(all_pwcurve)
## Power for predictor 'x', (95% confidence interval),
## by number of levels in g:
##       4: 46.00% (31.81, 60.68) - 40 rows
##       6: 74.00% (59.66, 85.37) - 60 rows
##       8: 92.00% (80.77, 97.78) - 80 rows
##      10: 98.00% (89.35, 99.95) - 100 rows
##      12: 100.0% (92.89, 100.0) - 120 rows
## 
## Time elapsed: 0 h 0 m 7 s
plot(all_pwcurve, xlab = 'Levels of g')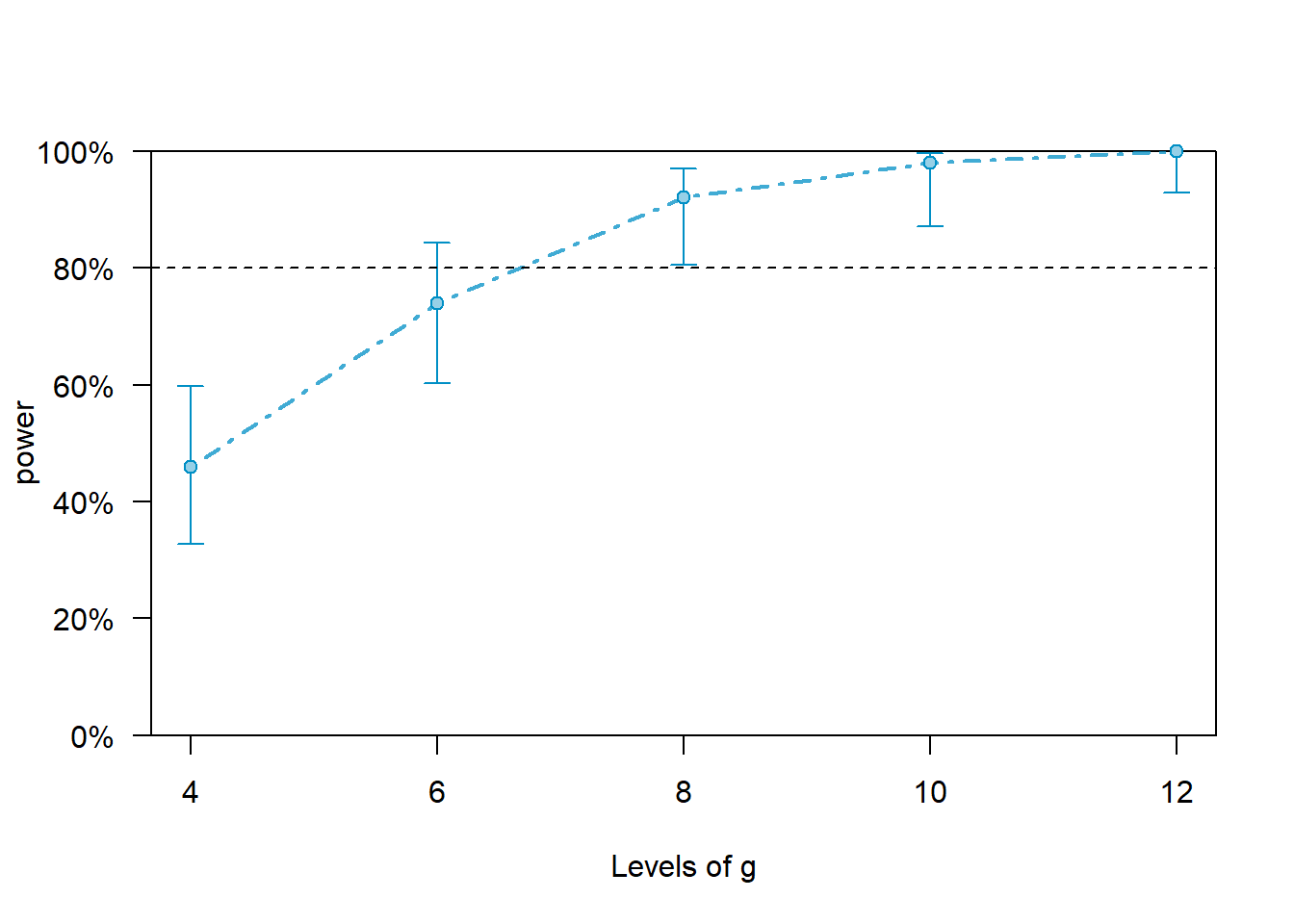

# For reproducibility purposes
sessionInfo()
## R version 4.2.3 (2023-03-15 ucrt)
## Platform: x86_64-w64-mingw32/x64 (64-bit)
## Running under: Windows 10 x64 (build 22621)
## 
## Matrix products: default
## 
## locale:
## [1] LC_COLLATE=English_United States.utf8 
## [2] LC_CTYPE=English_United States.utf8   
## [3] LC_MONETARY=English_United States.utf8
## [4] LC_NUMERIC=C                          
## [5] LC_TIME=English_United States.utf8    
## 
## attached base packages:
## [1] stats     graphics  grDevices utils     datasets  methods   base     
## 
## other attached packages:
## [1] simr_1.0.7          lme4_1.1-32         Matrix_1.5-3       
## [4] knitr_1.42          xaringanExtra_0.7.0
## 
## loaded via a namespace (and not attached):
##  [1] tidyselect_1.2.0 xfun_0.38        bslib_0.4.2      purrr_1.0.1     
##  [5] splines_4.2.3    lattice_0.20-45  carData_3.0-5    vctrs_0.6.1     
##  [9] generics_0.1.3   htmltools_0.5.5  yaml_2.3.7       mgcv_1.8-42     
## [13] utf8_1.2.3       rlang_1.1.0      jquerylib_0.1.4  nloptr_2.0.3    
## [17] pillar_1.9.0     glue_1.6.2       uuid_1.1-0       plyr_1.8.8      
## [21] binom_1.1-1.1    lifecycle_1.0.3  stringr_1.5.0    blogdown_1.16   
## [25] evaluate_0.21    fastmap_1.1.1    RLRsim_3.1-8     parallel_4.2.3  
## [29] pbkrtest_0.5.2   fansi_1.0.4      broom_1.0.4      Rcpp_1.0.10     
## [33] backports_1.4.1  plotrix_3.8-2    cachem_1.0.7     jsonlite_1.8.4  
## [37] abind_1.4-5      digest_0.6.31    stringi_1.7.12   bookdown_0.33.3 
## [41] dplyr_1.1.1      grid_4.2.3       cli_3.4.1        tools_4.2.3     
## [45] magrittr_2.0.3   sass_0.4.6       tibble_3.2.1     tidyr_1.3.0     
## [49] car_3.1-2        pkgconfig_2.0.3  MASS_7.3-58.3    minqa_1.2.5     
## [53] rmarkdown_2.21   rstudioapi_0.14  iterators_1.0.14 R6_2.5.1        
## [57] boot_1.3-28.1    nlme_3.1-162     compiler_4.2.3


Just the code


library(lme4)
library(simr)

# Toy model
fm = lmer(y ~ x + (x | g), data = simdata)

# Extend sample size of `g`
fm_extended_g = extend(fm, along = 'g', n = 12)

# Parallelize `breaks` by running each number of levels in a separate function.

# 4 levels of g
pwcurve_4g = powerCurve(fm_extended_g, fixed('x'), along = 'g', breaks = 4, 
                        nsim = 50, seed = 123, 
                        # No progress bar
                        progress = FALSE)

# 6 levels of g
pwcurve_6g = powerCurve(fm_extended_g, fixed('x'), along = 'g', breaks = 6, 
                        nsim = 50, seed = 123, 
                        # No progress bar
                        progress = FALSE)

# 8 levels of g
pwcurve_8g = powerCurve(fm_extended_g, fixed('x'), along = 'g', breaks = 8, 
                        nsim = 50, seed = 123, 
                        # No progress bar
                        progress = FALSE)

# 10 levels of g
pwcurve_10g = powerCurve(fm_extended_g, fixed('x'), along = 'g', breaks = 10, 
                        nsim = 50, seed = 123, 
                        # No progress bar
                        progress = FALSE)

# 12 levels of g
pwcurve_12g = powerCurve(fm_extended_g, fixed('x'), along = 'g', breaks = 12, 
                        nsim = 50, seed = 123, 
                        # No progress bar
                        progress = FALSE)


# Create a destination object using any of the power curves above.
all_pwcurve = pwcurve_4g

# Combine results
all_pwcurve$ps = c(pwcurve_4g$ps[1], pwcurve_6g$ps[1], pwcurve_8g$ps[1], 
                   pwcurve_10g$ps[1], pwcurve_12g$ps[1])

# Combine the different numbers of levels.
all_pwcurve$xval = c(pwcurve_4g$nlevels, pwcurve_6g$nlevels, pwcurve_8g$nlevels, 
                     pwcurve_10g$nlevels, pwcurve_12g$nlevels)


print(all_pwcurve)

plot(all_pwcurve, xlab = 'Levels of g')


References

Brysbaert, M., & Stevens, M. (2018). Power analysis and effect size in mixed effects models: A tutorial. Journal of Cognition, 1(1), 9. http://doi.org/10.5334/joc.10

Green, P., & MacLeod, C. J. (2016). SIMR: An R package for power analysis of generalized linear mixed models by simulation. Methods in Ecology and Evolution 7(4), 493–498, https://doi.org/10.1111/2041-210X.12504

Kumle, L., Vo, M. L. H., & Draschkow, D. (2021). Estimating power in (generalized) linear mixed models: An open introduction and tutorial in R. Behavior Research Methods, 1–16. https://doi.org/10.3758/s13428-021-01546-0

Luke, S. G. (2017). Evaluating significance in linear mixed-effects models in R. Behavior Research Methods, 49(4), 1494–1502. https://doi.org/10.3758/s13428-016-0809-y


  1. The number of simulations set by nsim should be larger (Brysbaert & Stevens, 2018; Green & MacLeod, 2016). In addition, the effect size for x should be adjusted to the value that best fits with the planned study (Kumle et al., 2021).↩︎

s power analysis
comments powered by Disqus