A new function to plot convergence diagnostics from lme4::allFit()
Linear mixed-effects models (LMM) offer a consistent way of performing regression and analysis of variance tests which allows accounting for non-independence in the data. Over the past decades, LMMs have subsumed most of the General Linear Model, with a steady increase in popularity (Meteyard & Davies, 2020). Since their conception, LMMs have presented the challenge of model convergence. In essence, the issue of convergence boils down to the widespread tension between parsimony and completeness in data analysis. That is, on the one hand, a good model must allow an accurate, parsimonious analysis of each predictor, and thus, it must not be overfitted with too many parameters. Yet, on the other hand, the model must be complete enough to account for a sufficient amount of variation in the data. In LMMs, any predictors that entail non-independent observations (also known as repeated measures) will normally bring both fixed and random effects into the model. Where a few of these predictors coexist, models often struggle to find enough information in the data to account for every predictor—and especially, for every random effect. This difficulty translates into convergence warnings (Brauer & Curtin, 2018; Singmann & Kellen, 2019). In this article, I review the issue of convergence before presenting a new plotting function in R that facilitates the diagnosis of convergence by visualising the fixed effects fitted by different optimization algorithms (also dubbed optimizers).
Completeness versus parsimony
Both fixed and random effects comprise intercepts and slopes. The pressure exerted by each of those types of effects on the model is determined by the number of data points involved by each. First, slopes are more demanding than intercepts, as they involve a (far) larger number of data points. Second, random effects are more demanding than fixed effects, as random effects entail the number of estimates required for fixed effects times the number of levels in the grouping factor. As a result, on the most lenient end of the scale lies the fixed intercept, and on the heaviest end lie the random slopes. Convergence warnings in LMMs are often due to the random slopes alone.
Sounds easy, then! Not inviting the random slopes to the party should solve the problem. Indeed, since random slopes involve the highest number of estimates by far, removing them does often remove convergence warnings. This, however, leads to a different problem. Surrendering the information provided by random slopes can result in the violation of the assumption of independence of observations. For years, the removal of random slopes due to convergence warnings was standard practice. Currently, in contrast, proposals increasingly consider other options, such as removing random effects if they do not significantly improve the fit of the model (Matuschek et al., 2017), and keeping the random slopes in the model in spite of the convergence warnings to safeguard the assumption of independence (see Table 17 in Brauer & Curtin, 2018; Singmann & Kellen, 2019).
The multiple-optimizers sanity check from lme4::allFit()
Framed within the drive to maintain random slopes wherever possible, the developers of the ‘lme4’ package propose a sanity check that uses a part of the ‘lme4’ engine called ‘optimizer’. Every model has a default optimizer, unless a specific one is chosen through control = lmerControl(optimizer = '...') (in lmer models) or control = glmerControl(optimizer = '...') (in glmer models). The seven widely-available optimizers are:
- bobyqa
- Nelder_Mead
- nlminbwrap
- nmkbw
- optimx.L-BFGS-B
- nloptwrap.NLOPT_LN_NELDERMEAD
- nloptwrap.NLOPT_LN_BOBYQA
To assess whether convergence warnings render the results invalid, or on the contrary, the results can be deemed valid in spite of the warnings, Bates et al. (2022) suggest refitting models affected by convergence warnings with a variety of optimizers. The authors argue that if the different optimizers produce practically-equivalent results, the results are valid. The allFit function from the ‘lme4’ package allows the refitting of models using a number of optimizers. To use the seven optimizers listed above, two extra packages must be installed: ‘dfoptim’ and ‘optimx’ (see lme4 manual). The output from allFit() contains several statistics on the fixed and the random effects fitted by each optimizer (see example).
Plotting the fixed effects from allFit()
Several R users have ventured into plotting the allFit() output but there is not a function in ‘lme4’ yet at the time of writing. I (Bernabeu, 2022) developed a function that takes the output from allFit(), tidies it, selects the fixed effects and plots them using ‘ggplot2’. The function is shown below, and can be copied through the Copy Code button at the top right corner. It can be renamed by changing plot.fixef.allFit to another valid name.
# Plot the results from the fixed effects produced by different optimizers. This function
# takes the output from lme4::allFit(), tidies it, selects fixed effects and plots them.
plot.fixef.allFit = function(allFit_output,
# Set the same Y axis limits in every plot
shared_y_axis_limits = TRUE,
# Multiply Y axis limits by a factor (only
# available if shared_y_axis_limits = TRUE)
multiply_y_axis_limits = 1,
# Number of decimal places
decimal_places = NULL,
# Select predictors
select_predictors = NULL,
# Number of rows
nrow = NULL,
# Y axis title
y_title = 'Fixed effect',
# Alignment of the Y axis title
y_title_hjust = NULL,
# Add number to the names of optimizers
number_optimizers = TRUE,
# Replace colon in interactions with x
interaction_symbol_x = TRUE) {
require(lme4)
require(dfoptim)
require(optimx)
require(dplyr)
require(reshape2)
require(stringr)
require(scales)
require(ggplot2)
require(ggtext)
require(patchwork)
library(Cairo)
# Tidy allFit output
# Extract fixed effects from the allFit() output
allFit_fixef = summary(allFit_output)$fixef %>% # Select fixed effects in the allFit results
reshape2::melt() %>% # Structure the output as a data frame
rename('Optimizer' = 'Var1', 'fixed_effect' = 'Var2') # set informative names
# If number_optimizers = TRUE, assign number to each optimizer and place it before its name
if(number_optimizers == TRUE) {
allFit_fixef$Optimizer = paste0(as.numeric(allFit_fixef$Optimizer), '. ', allFit_fixef$Optimizer)
}
# If select_predictors was supplied, select them along with the intercept (the latter required)
if(!is.null(select_predictors)) {
allFit_fixef = allFit_fixef %>% dplyr::filter(fixed_effect %in% c('(Intercept)', select_predictors))
}
# Order variables
allFit_fixef = allFit_fixef[, c('Optimizer', 'fixed_effect', 'value')]
# PLOT. The overall plot is formed of a first row containing the intercept and the legend
# (intercept_plot), and a second row containing the predictors (predictors_plot),
# which may in turn occupy several rows.
# If multiply_y_axis_limits was supplied but shared_y_axis_limits = FALSE,
# warn that shared_y_axis_limits is required.
if(!multiply_y_axis_limits == 1 & shared_y_axis_limits == FALSE) {
message('The argument `multiply_y_axis_limits` has not been used because \n it requires `shared_y_axis_limits` set to TRUE.')
}
# If extreme values were entered in y_title_hjust, show warning
if(!is.null(y_title_hjust)) {
if(y_title_hjust < 0.5 | y_title_hjust > 6) {
message('NOTE: For y_title_hjust, a working range of values is between 0.6 and 6.')
}
}
# If decimal_places was supplied, convert number to the format used in 'scales' package
if(!is.null(decimal_places)) {
decimal_places =
ifelse(decimal_places == 1, 0.1,
ifelse(decimal_places == 2, 0.01,
ifelse(decimal_places == 3, 0.001,
ifelse(decimal_places == 4, 0.0001,
ifelse(decimal_places == 5, 0.00001,
ifelse(decimal_places == 6, 0.000001,
ifelse(decimal_places == 7, 0.0000001,
ifelse(decimal_places == 8, 0.00000001,
ifelse(decimal_places == 9, 0.000000001,
ifelse(decimal_places == 10, 0.0000000001,
ifelse(decimal_places == 11, 0.00000000001,
ifelse(decimal_places == 12, 0.000000000001,
ifelse(decimal_places == 13, 0.0000000000001,
ifelse(decimal_places == 14, 0.00000000000001,
ifelse(decimal_places >= 15, 0.000000000000001,
0.001
)))))))))))))))
}
# First row: intercept_plot
# Select intercept data only
intercept = allFit_fixef %>% dplyr::filter(fixed_effect == '(Intercept)')
intercept_plot = intercept %>%
ggplot(., aes(fixed_effect, value, colour = Optimizer)) +
geom_point(position = position_dodge(1)) +
facet_wrap(~fixed_effect, scale = 'free') +
guides(colour = guide_legend(title.position = 'left')) +
theme_bw() +
theme(axis.title = element_blank(), axis.ticks.x = element_blank(),
axis.text.x = element_blank(),
strip.text = element_text(size = 10, margin = margin(t = 4, b = 6)),
strip.background = element_rect(fill = 'grey96'),
legend.margin = margin(0.3, 0, 0.8, 1, 'cm'),
legend.title = element_text(size = unit(15, 'pt'), angle = 90, hjust = 0.5))
# Second row: predictors_plot
# Select all predictors except intercept
predictors = allFit_fixef %>% dplyr::filter(!fixed_effect == '(Intercept)')
# If interaction_symbol_x = TRUE (default), replace colon with times symbol x between spaces
if(interaction_symbol_x == TRUE) {
# Replace colon in interactions with \u00D7, i.e., x; then set factor class
predictors$fixed_effect = predictors$fixed_effect %>%
str_replace_all(':', ' \u00D7 ') %>% factor()
}
# Order predictors as in the original output from lme4::allFit()
predictors$fixed_effect = factor(predictors$fixed_effect,
levels = unique(predictors$fixed_effect))
# Set number of rows for the predictors excluding the intercept.
# First, if nrow argument supplied, use it
if(!is.null(nrow)) {
predictors_plot_nrow = nrow - 1 # Subtract 1 as intercept row not considered
# Else, if nrow argument not supplied, calculate sensible number of rows: i.e., divide number of
# predictors (exc. intercept) by 2 and round up the result. For instance, 7 predictors --> 3 rows
} else predictors_plot_nrow = (length(unique(predictors$fixed_effect)) / 2) %>% ceiling()
predictors_plot = ggplot(predictors, aes(fixed_effect, value, colour = Optimizer)) +
geom_point(position = position_dodge(1)) +
facet_wrap(~fixed_effect, scale = 'free',
# Note that predictors_plot_nrow was defined a few lines above
nrow = predictors_plot_nrow,
# Wrap names of predictors with more than 54 characters into new lines
labeller = labeller(fixed_effect = label_wrap_gen(width = 55))) +
labs(y = y_title) +
theme_bw() +
theme(axis.title.x = element_blank(), axis.text.x = element_blank(),
axis.ticks.x = element_blank(),
axis.title.y = ggtext::element_markdown(size = 14, margin = margin(0, 15, 0, 0)),
strip.text = element_text(size = 10, margin = margin(t = 4, b = 6)),
strip.background = element_rect(fill = 'grey96'), legend.position = 'none')
# Below, the function scale_y_continuous is applied conditionally to avoid overriding settings. First,
# if shared_y_axis_limits = TRUE and decimal_places was supplied, set the same Y axis limits in
# every plot and set decimal_places. By default, also expand limits by a seventh of its original
# limit, and allow further multiplication of limits through multiply_y_axis_limits.
if(shared_y_axis_limits == TRUE & !is.null(decimal_places)) {
intercept_plot = intercept_plot +
scale_y_continuous(limits = c(min(allFit_fixef$value) - allFit_fixef$value %>% abs %>%
max / 7 * multiply_y_axis_limits,
max(allFit_fixef$value) + allFit_fixef$value %>% abs %>%
max / 7 * multiply_y_axis_limits),
# Set number of decimal places
labels = scales::label_number(accuracy = decimal_places))
predictors_plot = predictors_plot +
scale_y_continuous(limits = c(min(allFit_fixef$value) - allFit_fixef$value %>% abs %>%
max / 7 * multiply_y_axis_limits,
max(allFit_fixef$value) + allFit_fixef$value %>% abs %>%
max / 7 * multiply_y_axis_limits),
# Set number of decimal places
labels = scales::label_number(accuracy = decimal_places))
# Else, if shared_y_axis_limits = TRUE but decimal_places were not supplied, do as above but without
# setting decimal_places.
} else if(shared_y_axis_limits == TRUE & is.null(decimal_places)) {
intercept_plot = intercept_plot +
scale_y_continuous(limits = c(min(allFit_fixef$value) - allFit_fixef$value %>% abs %>%
max / 7 * multiply_y_axis_limits,
max(allFit_fixef$value) + allFit_fixef$value %>% abs %>%
max / 7 * multiply_y_axis_limits),
# Set number of decimal places
labels = scales::label_number(accuracy = decimal_places))
predictors_plot = predictors_plot +
scale_y_continuous(limits = c(min(allFit_fixef$value) - allFit_fixef$value %>% abs %>%
max / 7 * multiply_y_axis_limits,
max(allFit_fixef$value) + allFit_fixef$value %>% abs %>%
max / 7 * multiply_y_axis_limits),
# Set number of decimal places
labels = scales::label_number(accuracy = decimal_places))
# Else, if shared_y_axis_limits = FALSE and decimal_places was supplied, set decimal_places.
} else if(shared_y_axis_limits == FALSE & !is.null(decimal_places)) {
# Set number of decimal places in both plots
intercept_plot = intercept_plot +
scale_y_continuous(labels = scales::label_number(accuracy = decimal_places))
predictors_plot = predictors_plot +
scale_y_continuous(labels = scales::label_number(accuracy = decimal_places))
}
# Plot matrix: based on number of predictors_plot_nrow, adjust height of Y axis title
# (unless supplied), and assign space to intercept_plot and predictors_plot
if(predictors_plot_nrow == 1) {
# If y_title_hjust supplied, use it
if(!is.null(y_title_hjust)) {
predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = y_title_hjust))
# Otherwise, set a sensible height
} else predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = 3.6))
layout = c(
patchwork::area(t = 1.5, r = 8.9, b = 6.8, l = 0), # intercept row
patchwork::area(t = 7.3, r = 9, b = 11, l = 0) # predictors row(s)
)
} else if(predictors_plot_nrow == 2) {
# If y_title_hjust supplied, use it
if(!is.null(y_title_hjust)) {
predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = y_title_hjust))
# Otherwise, set a sensible height
} else predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = 1.4))
layout = c(
patchwork::area(t = 1.5, r = 8.9, b = 6.8, l = 0), # intercept row
patchwork::area(t = 7.3, r = 9, b = 16, l = 0) # predictors row(s)
)
} else if(predictors_plot_nrow == 3) {
# If y_title_hjust supplied, use it
if(!is.null(y_title_hjust)) {
predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = y_title_hjust))
# Otherwise, set a sensible height
} else predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = 0.92))
layout = c(
patchwork::area(t = 1.5, r = 8.9, b = 6.8, l = 0), # intercept row
patchwork::area(t = 7.3, r = 9, b = 21, l = 0) # predictors row(s)
)
} else if(predictors_plot_nrow == 4) {
# If y_title_hjust supplied, use it
if(!is.null(y_title_hjust)) {
predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = y_title_hjust))
# Otherwise, set a sensible height
} else predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = 0.8))
layout = c(
patchwork::area(t = 1.5, r = 8.9, b = 6.8, l = 0), # intercept row
patchwork::area(t = 7.3, r = 9, b = 26, l = 0) # predictors row(s)
)
} else if(predictors_plot_nrow == 5) {
# If y_title_hjust supplied, use it
if(!is.null(y_title_hjust)) {
predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = y_title_hjust))
# Otherwise, set a sensible height
} else predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = 0.73))
layout = c(
patchwork::area(t = 1.5, r = 8.9, b = 6.8, l = 0), # intercept row
patchwork::area(t = 7.3, r = 9, b = 31, l = 0) # predictors row(s)
)
} else if(predictors_plot_nrow > 5) {
# If y_title_hjust supplied, use it
if(!is.null(y_title_hjust)) {
predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = y_title_hjust))
# Otherwise, set a sensible height
} else predictors_plot = predictors_plot +
theme(axis.title.y = ggtext::element_markdown(hjust = 0.65))
layout = c(
patchwork::area(t = 1.5, r = 8.9, b = 6.8, l = 0), # intercept row
patchwork::area(t = 7.3, r = 9, b = 36, l = 0) # predictors row(s)
)
# Also, advise user to consider distributing predictors into several plots
message(' Many rows! Consider distributing predictors into several plots \n using argument `select_predictors`')
}
# Add margin
predictors_plot = predictors_plot + theme(plot.margin = margin(15, 15, 15, 15))
# Return matrix of plots
wrap_plots(intercept_plot, predictors_plot, design = layout,
# The 2 below corresponds to intercept_plot and predictors_plot
nrow = 2)
}Optional arguments
Below are the optional arguments allowed by the function, with their default values.
# Set the same Y axis limits in every plot
shared_y_axis_limits = TRUE,
# Multiply Y axis limits by a factor (only
# available if shared_y_axis_limits = TRUE)
multiply_y_axis_limits = 1,
# Number of decimal places
decimal_places = NULL,
# Select predictors
select_predictors = NULL,
# Number of rows
nrow = NULL,
# Y axis title
y_title = 'Fixed effect',
# Alignment of the Y axis title
y_title_hjust = NULL,
# Add number to the names of optimizers
number_optimizers = TRUE,
# Replace colon in interactions with x
interaction_symbol_x = TRUE
The argument shared_y_axis_limits deserves a comment. It allows using the same Y axis limits (i.e., range) in all plots or, alternatively, using plot-specific limits. The parameter is TRUE by default to prevent overinterpretations of small differences across optimizers (see the first figure below). In contrast, when shared_y_axis_limits = FALSE, plot-specific limits are used, which results in a narrower range of values in the Y axis (see the second figure below). Since data points will span the entire Y axis in that case, any difference across optimizers—regardless of its relative importance—might be perceived as large, unless the specific range of values in each plot is noticed.
Use case
Let’s test the function with a minimal model.
# Create data using code by Ben Bolker from
# https://stackoverflow.com/a/38296264/7050882
set.seed(101)
spin = runif(600, 1, 24)
reg = runif(600, 1, 15)
ID = rep(c("1","2","3","4","5", "6", "7", "8", "9", "10"))
day = rep(1:30, each = 10)
testdata <- data.frame(spin, reg, ID, day)
testdata$fatigue <- testdata$spin * testdata$reg/10 * rnorm(30, mean=3, sd=2)
# Model
library(lme4)
fit = lmer(fatigue ~ spin * reg + (1|ID),
data = testdata, REML = TRUE)
# Refit model using all available algorithms
multi_fit = allFit(fit)## bobyqa : [OK]
## Nelder_Mead : [OK]
## nlminbwrap : [OK]
## nmkbw : [OK]
## optimx.L-BFGS-B : [OK]
## nloptwrap.NLOPT_LN_NELDERMEAD : [OK]
## nloptwrap.NLOPT_LN_BOBYQA : [OK]summary(multi_fit)$fixef## (Intercept) spin reg spin:reg
## bobyqa -2.975678 0.5926561 0.1437204 0.1834016
## Nelder_Mead -2.975675 0.5926559 0.1437202 0.1834016
## nlminbwrap -2.975677 0.5926560 0.1437203 0.1834016
## nmkbw -2.975678 0.5926561 0.1437204 0.1834016
## optimx.L-BFGS-B -2.975680 0.5926562 0.1437205 0.1834016
## nloptwrap.NLOPT_LN_NELDERMEAD -2.975666 0.5926552 0.1437196 0.1834017
## nloptwrap.NLOPT_LN_BOBYQA -2.975678 0.5926561 0.1437204 0.1834016The effects to be visualised are selected below using the argument select_predictors. Notice that the intercept is plotted by default on the first row, along with the legend that lists all the optimizers used.
# Read in function from GitHub
source('https://raw.githubusercontent.com/pablobernabeu/plot.fixef.allFit/main/plot.fixef.allFit.R')
plot.fixef.allFit(multi_fit,
select_predictors = c('spin', 'reg', 'spin:reg'),
# Increase padding at top and bottom of Y axis
multiply_y_axis_limits = 1.3,
y_title = 'Fixed effect (*b*)',
# Align y title
y_title_hjust = .9)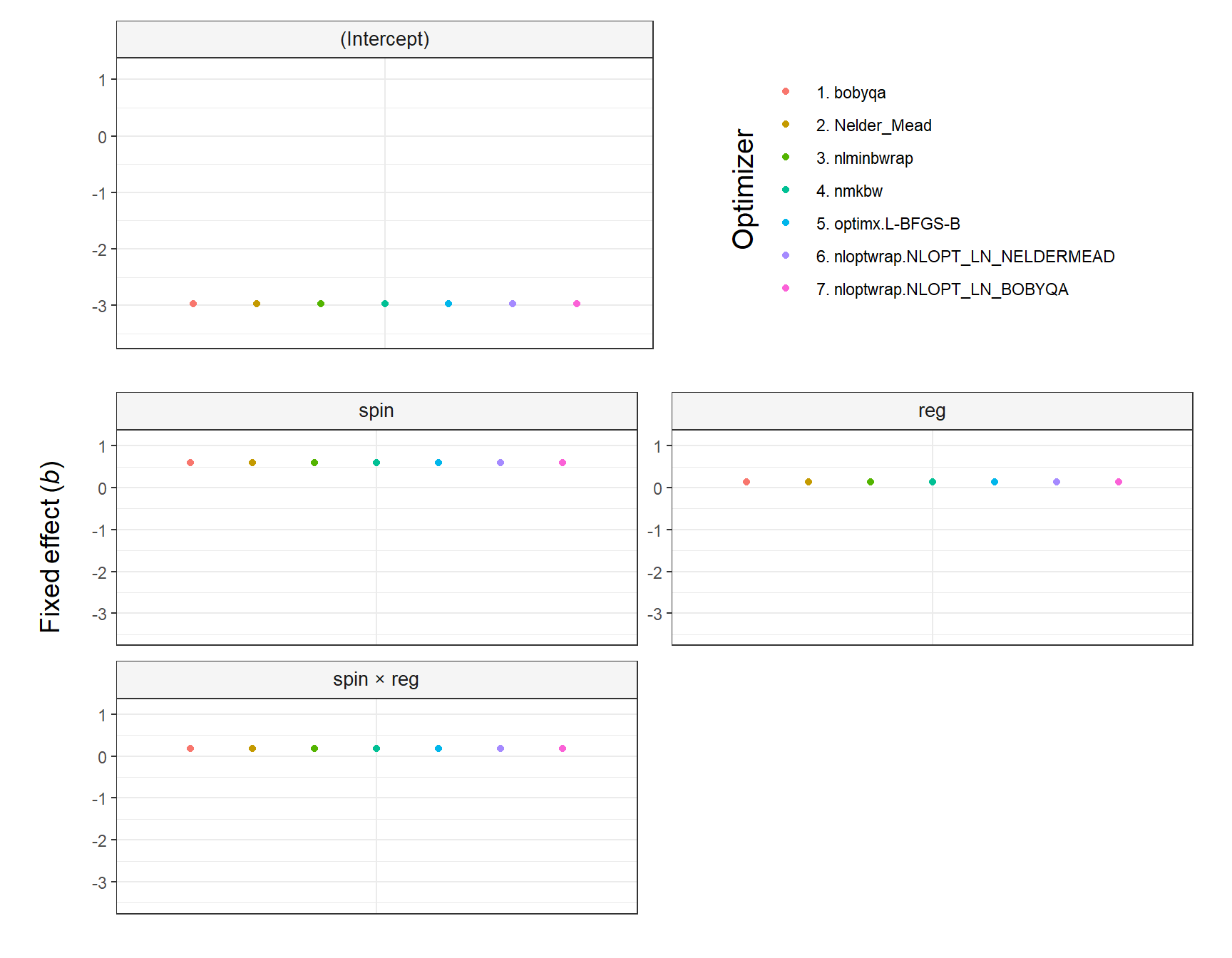
The plot produced by plot.fixef.allFit() by default replaces the colons in interaction effects (e.g., spin:reg) with ’ × ’ to facilitate the visibility (this can be overriden by setting interaction_symbol_x = FALSE). Yet, it is important to note that any interactions passed to select_predictors must have the colon, as that is the symbol present in the lme4::allFit() output.
The output of plot.fixef.allFit() is a ggplot2 object that can be stored for further use, as in the example below, in which new parameters are used.
library(ggplot2)
plot_fit_convergence =
plot.fixef.allFit(multi_fit,
select_predictors = c('spin', 'spin:reg'),
# Use plot-specific Y axis limits
shared_y_axis_limits = FALSE,
decimal_places = 7,
# Move up Y axis title
y_title_hjust = -20,
y_title = 'Fixed effect (*b*)')
# Print
plot_fit_convergence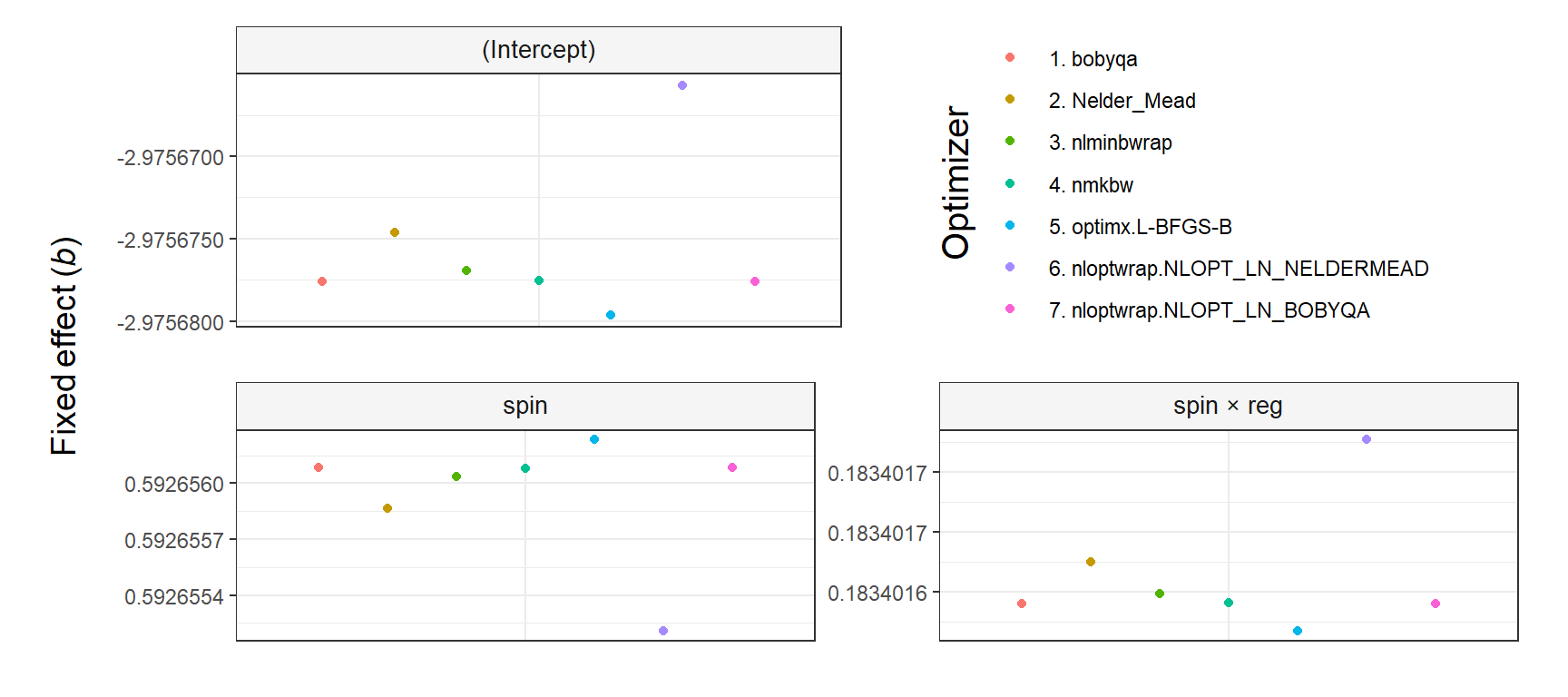
# Plot can be saved to disk as pdf, png, etc. through `ggplot2::ggsave()`
# ggsave('plot_fit_convergence.pdf', plot_fit_convergence,
# device = cairo_pdf, width = 9, height = 9, dpi = 900)References
Bates, D., Maechler, M., Bolker, B., Walker, S., Christensen, R. H. B., Singmann, H., Dai, B., Scheipl, F., Grothendieck, G., Green, P., Fox, J., Bauer, A., & Krivitsky, P. N. (2022). Package ‘lme4’. CRAN. https://cran.r-project.org/web/packages/lme4/lme4.pdf
Bernabeu, P. (2022). Language and sensorimotor simulation in conceptual processing: Multilevel analysis and statistical power. Lancaster University. https://doi.org/10.17635/lancaster/thesis/1795
Brauer, M., & Curtin, J. J. (2018). Linear mixed-effects models and the analysis of nonindependent data: A unified framework to analyze categorical and continuous independent variables that vary within-subjects and/or within-items. Psychological Methods, 23(3), 389–411. https://doi.org/10.1037/met0000159
Matuschek, H., Kliegl, R., Vasishth, S., Baayen, H., & Bates, D. (2017). Balancing type 1 error and power in linear mixed models. Journal of Memory and Language, 94, 305–315. https://doi.org/10.1016/j.jml.2017.01.001
Meteyard, L., & Davies, R. A. (2020). Best practice guidance for linear mixed-effects models in psychological science. Journal of Memory and Language, 112, 104092. https://doi.org/10.1016/j.jml.2020.104092
Singmann, H., & Kellen, D. (2019). An introduction to mixed models for experimental psychology. In D. H. Spieler & E. Schumacher (Eds.), New methods in cognitive psychology (pp. 4–31). Psychology Press.
Pablo Bernabeu
Postdoctoral fellow at UiT –
The Arctic University of Norway
After doing a research master's, I became a PhD student and graduate teaching assistant in Psychology at Lancaster University, where I investigated how conceptual processing—that is, the comprehension of the meaning of words—is supported by linguistic and sensorimotor brain systems, and how research on this topic is influenced by methodological aspects such as the operationalisation of variables and the sample size of experiments. Currently, I am a postdoctoral fellow at UiT The Arctic University of Norway, where I am investigating the behavioural and neural underpinnings of multilingualism. Throughout my research, I have used methods such as behavioural and electroencephalographic experiments, corpus analysis, statistics and programming. Research materials at https://osf.io/25u3x. CV available here.